Phân tích một số ra thừa số nguyên tố là chuyên đề quan trọng trong chương trình toán 6 THCS. Vì thế, để giải quyết được các dạng bài tập của chủ đề này, bạn cần nắm vững kiến thức lý thuyết cũng như các dạng toán để giải quyết được một số ra thừa số nguyên tố. Trong nội dung chi tiết dưới đây, hãy cùng DINHNGHIA.COM.VN tìm hiểu chi tiết về chuyên đề phân tích số ra thừa số nguyên tố nhé!
Nội dung bài viết
Nhắc lại về khái niệm số nguyên tố
Số nguyên tố theo định nghĩa chính là số tự nhiên lớn hơn 1, và chỉ có 2 ước số dương là 1 và chính nó. Hay nói cách khác thì số nguyên tố là số chỉ chia hết cho 1 và chính nó mà thôi. Ví dụ các số 2, 3, 5, 7, 11 là những số nguyên tố điển hình trong toán học.
Để kết luận a là số nguyên tố (a > 1) thì ta chỉ cần chứng tỏ rằng nó không chia hết cho mọi số nguyên tố mà bình phương không vượt quá a.

Khái niệm phân tích số ra thừa số nguyên tố
Thừa số nguyên tố theo định nghĩa là tích các số nguyên tố, có thể viết số đó dưới dạng một tích các thừa số nguyên tố.
Như vậy thì phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố chính là viết số đó dưới dạng một tích của các thừa số nguyên tố.
Các bước phân tích một số ra thừa số nguyên tố
- Bước 1: Đầu tiên, ta cần kiểm tra xem 2 có phải là ước của a hay không.
- Bước 2: Nếu không ta xét số nguyên tố 3 và cứ như thế đối với các số nguyên tố lớn dần.
- Bước 3: Giả sử p là ước nguyên tố nhỏ nhất của a, ta chia a cho p được thương b.
- Bước 4: Tiếp tục thực hiện quy trình trên đối với b.
- Bước 5: Quy trình trên vẫn tiếp tục cho đến khi ta được thương là một số nguyên tố.

Ta có thể phân tích theo sơ đồ cây hoặc theo sơ đồ hàng dọc.
Quy tắc hàng dọc: Khi ta chia số n cho một số nguyên tố (xét từ nhỏ đến lớn), sau đó chia thương tìm được cho một số nguyên tố (cũng xét từ nhỏ cho đến lớn), tiếp tục như vậy cho đến khi thương bằng 1.
Các cách phân tích một số để ra thừa số nguyên tố
Ví dụ: Hãy phân tích số 200 ra thừa số nguyên tố
Dạng 1: Theo sơ đồ hàng dọc
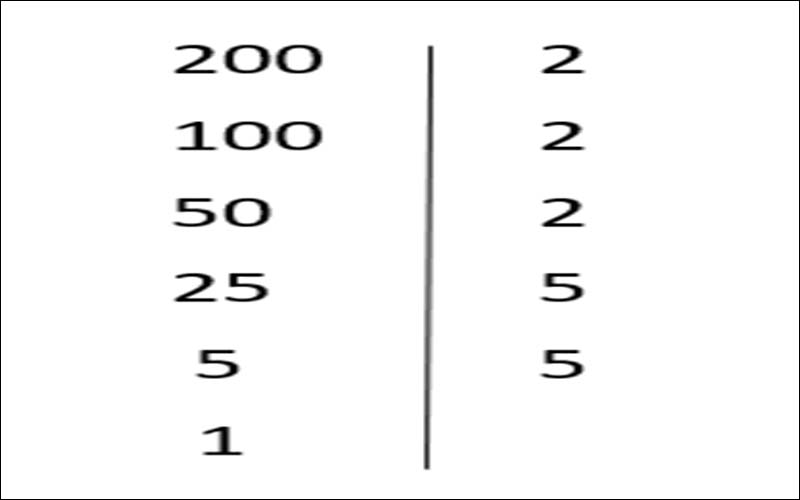
Dạng 2: Theo sơ đồ hình cây
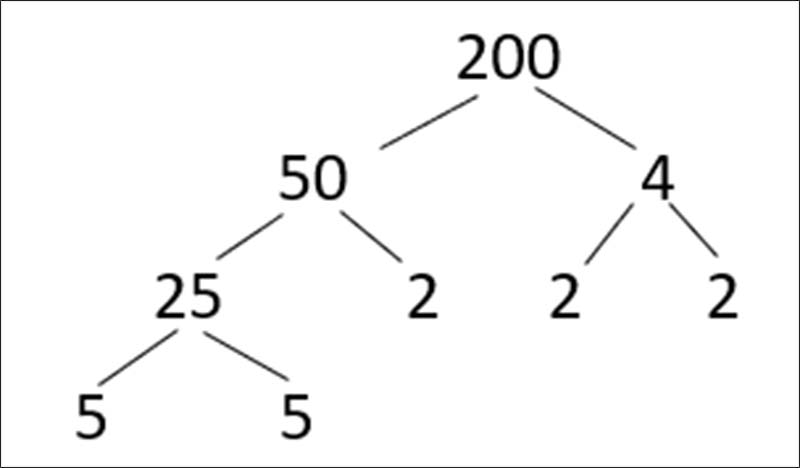
Cách tính số lượng các ước của một số m (m > 1)
Cách tính số lượng ước của một số m (m > 1): Ta xét dạng phân tích của số m ra thừa số nguyên tố:
- Nếu m=ax thì m có x + 1 ước.
- Nếu m=ax∗by thì m có (x+1)(y+1) ước.
- m=ax∗by∗cz thì có (x+1)(y+1)(z+1) ước.
Một số lưu ý khi phân tích 1 số ra thừa số nguyên tố
Ta nên lần lượt xét tính chia hết cho các số nguyên tố từ nhỏ đến lớn: 2, 3, 5, 7, 11,….
Trong quá trình xét tính chia hết nên vận dụng các dấu hiệu chia hết cho 2, 3, 5 đã được học từ các bài trước.
Khi phân tích số để ra thừa số nguyên tố theo cột dọc cần tuân thủ nguyên tắc: các số nguyên tố được viết bên phải cột, các thương được viết bên trái cột.
Dù phân tích một số tự nhiên ra thừa số nguyên tố bằng cách nào thì cũng đều cho cùng một kết quả.
Các dạng bài tập phân tích một số ra thừa số nguyên tố
Dạng 1: Phân tích các số cho trước ra thừa số nguyên tố
Phương pháp giải: Để giải được bài tập dạng này ta chia số đã cho theo dạng cột hoặc dạng cây.
Ví dụ: Cho tập hợp A = {70; 40; 350}. Phân tích từng phần tử trong tập A ra thừa số nguyên tố theo sơ đồ cây
Cách giải:
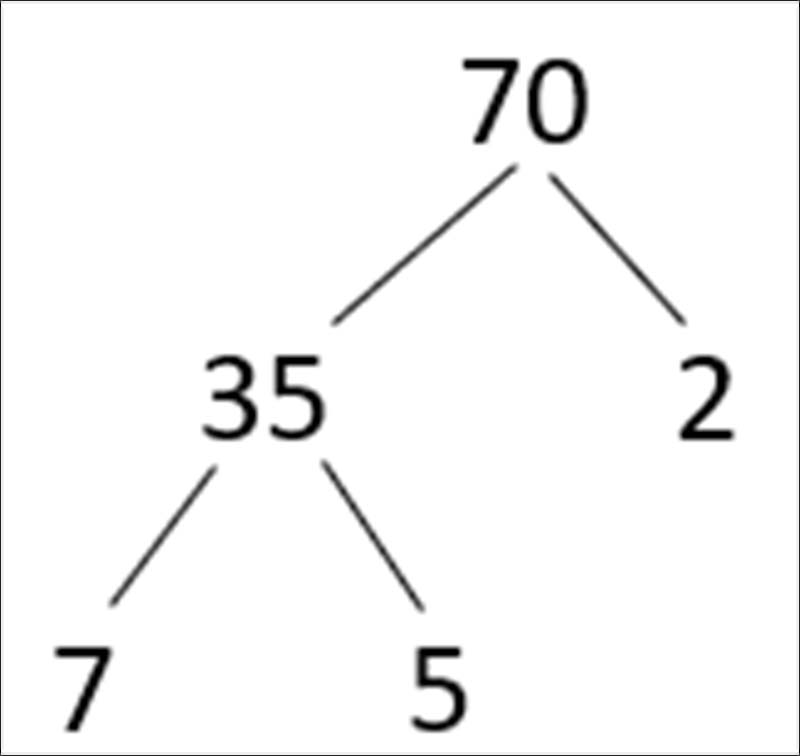
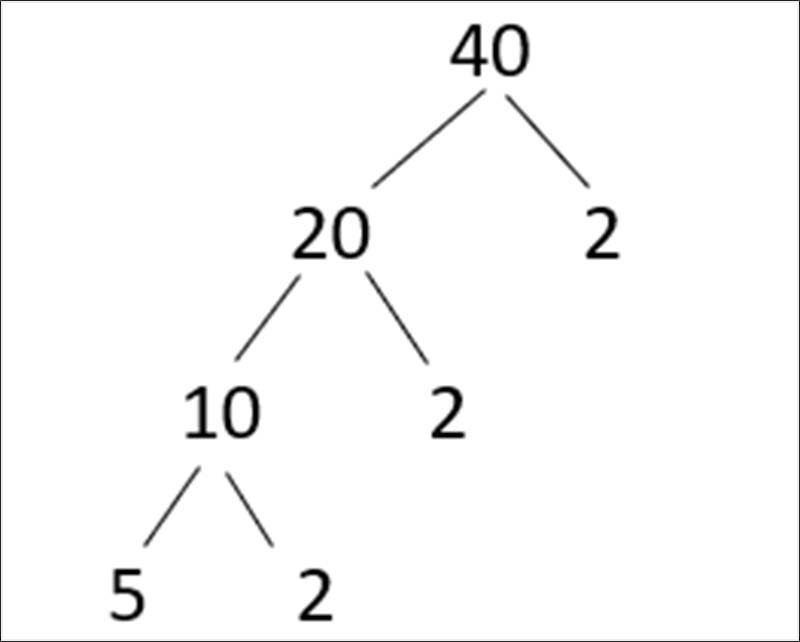
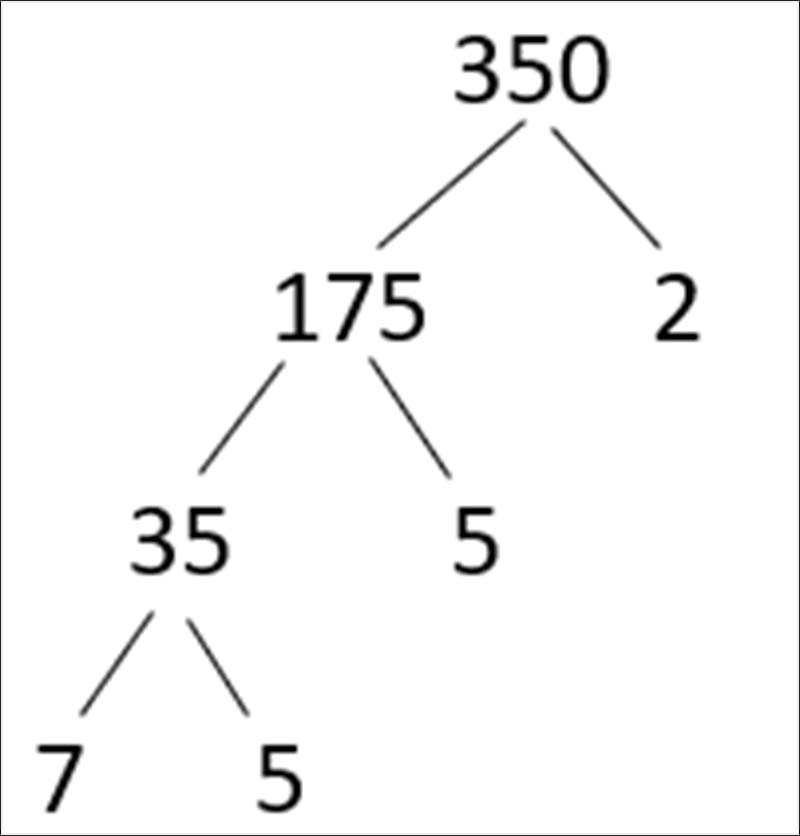
Dạng 2: Tìm hiểu về bài toán ứng dụng để tìm ước của một số
Phương pháp giải: Phân tích số cho trước ra thừa số nguyên tố. Chú ý rằng nếu c=a∗b thì a và b là hai ước của c.
Ví dụ 1: Cho các số sau 225, 1800, 1050, 3060. Phân tích các số sau ra thừa số nguyên tố rồi cho biết mỗi số đó chia hết cho các số nguyên tố nào?
Cách giải
- 225 = 32.52 ; 225 chia hết cho các số nguyên tố 3 và 5.
- 1800 = 23.32.52 ; 1800 chia hết cho các số nguyên tố 2, 3, 5.
- 1050 = 2.3.52.7 ; 1050 chia hết cho các số nguyên tố 2, 3, 5, 7.
- 3060 = 22.32.5.17 ; 3060 chia hết cho các số nguyên tố 2, 3, 5,17.
Dạng 3: Bài toán đưa về việc phân tích số ra thừa số nguyên tố
Phương pháp giải: Ta cần phân tích đề bài, đồng thời đưa về việc tìm ước của một số trước bằng cách phân tích số đó ra thừa số nguyên tố.
Ví dụ 1: An có 28 viên bi. An muốn xếp số bi đó vào túi sao cho số bi ở các túi đều bằng nhau . Hỏi An có thể xếp 28 viên bi đó vào mấy túi? (kể cả trường hợp xếp vào một túi).
Cách giải:
Số túi là ước của 28. Vậy 1, 2, 4, 7, 14, 28 túi.
Ví dụ 2: Phân tích 111 ra thừa số nguyên tố rồi tìm tập hợp các ước của 111.
Cách giải:
111=3∗37. Ư(11) = {1; 3; 37; 111}.
Tìm hiểu phân tích số ra thừa số nguyên tố pascal
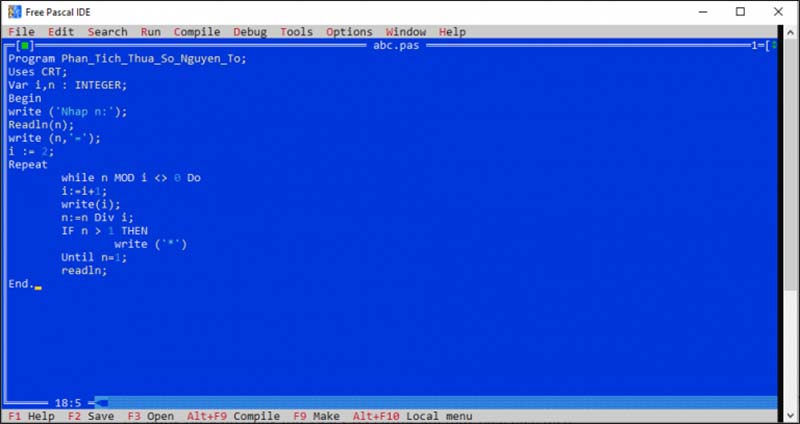
Xem thêm:
- Tìm hiểu những ứng dụng của Parabol trong đời sống thực tế
- Chuyên đề hệ thức Viet và ứng dụng: Lý thuyết và Bài tập
- Định nghĩa số nguyên tố là gì? Số siêu nguyên tố? 2 số nguyên tố cùng nhau?
Như vậy, bài viết trên đây của DINHNGHIA.VN đã cùng bạn tìm hiểu một cách chi tiết và cụ thể về chuyên đề phân tích một số nhằm ra thừa số nguyên tố. Hy vọng kiến thức trong bài viết đã mang đến cho bạn những cách hay khi phân tích một số ra thừa số nguyên tố. Chúc bạn luôn học và ôn thi thật tốt!


