Lý thuyết về hình trụ tròn là phần kiến thức quan trọng trong chương trình toán học THCS. Vậy hình trụ tròn là gì? Công thức tính diện tích hình trụ tròn như nào?… Trong nội dung bài viết dưới đây, hãy cùng DINHNGHIA.COM.VN tìm hiểu chi tiết nhé!
Nội dung bài viết
Hình trụ tròn là gì? Cách tính diện tích hình trụ tròn
Định nghĩa: Hình trụ tròn là hình trụ có 2 đáy là hình tròn bằng nhau và song song với nhau.
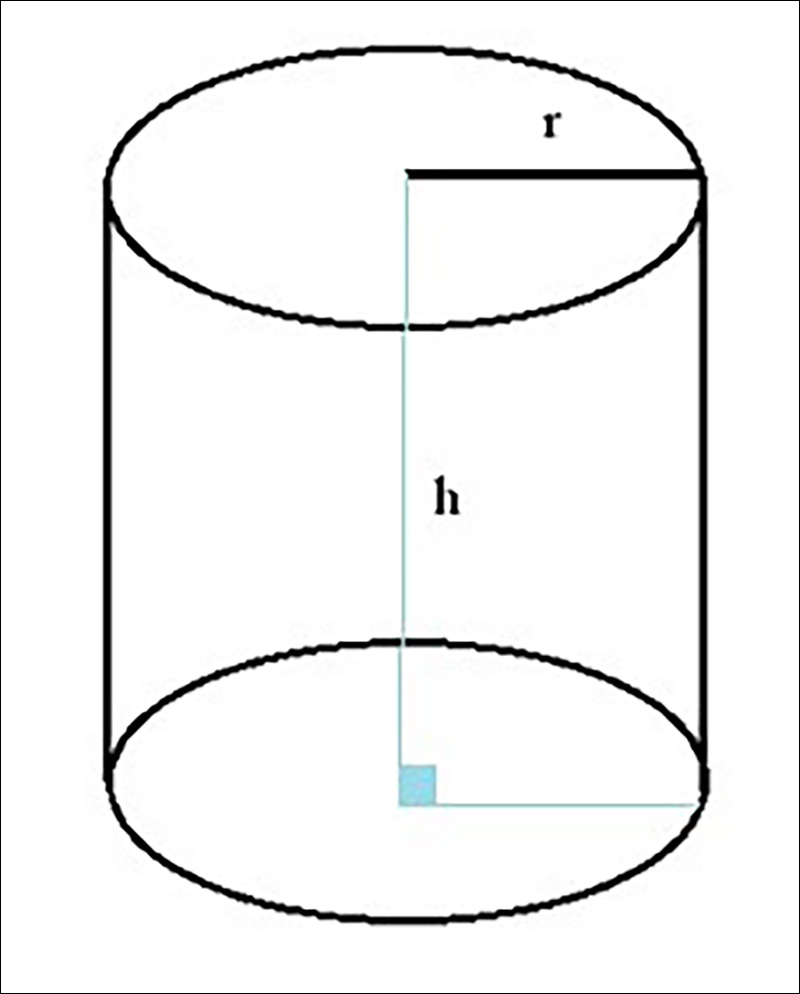
Trong đó:
- r là bán kính đường tròn đáy
- h là chiều cao hình trụ tròn
- (pi = 3,14)
Công thức tính diện tích hình trụ tròn
Muốn tính diện tích toàn phần của hình trụ tròn, ta cần tính diện tích 2 mặt đáy rồi cộng với diện tích xung quanh của nó.
=> Diện tích hình trụ tròn ((S_{tp})) = Diện tích xung quanh ((S_{xq})) + Diện tích 2 đáy ((S_{d}))
Diện tích đáy của hình trụ tròn
Diện tích đáy là diện tích của cả 2 đáy trên và đáy dưới.
Công thức: (S_{d} = pi. r^{2})
Diện tích xung quanh hình trụ tròn xoay
Diện tích xung quanh là phần diện tích bao quanh hình trụ tròn, không bao gồm diện tích của cả 2 đáy.
Công thức: (S_{xq} = 2pi rh)
Diện tích toàn phần của hình trụ tròn
(S_{tp} = S_{xq} + S_{d} = 2pi rh + 2pi r^{2})
Phương trình Descartes của hình trụ tròn
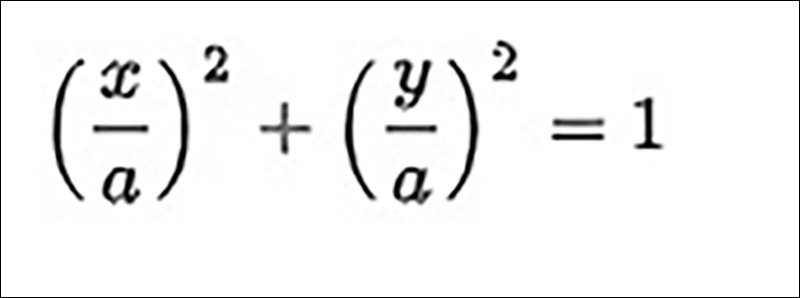
Có thể bạn quan tâm:
- 1 độ bằng bao nhiêu phút, giây, radian? Cách đổi đơn vị độ (góc)
- Cách đổi mm sang m chính xác nhất bằng công cụ chuyển đổi
- Mét vuông đổi ra mét bằng bao nhiêu? Có đổi được không?
Công thức tính thể tích hình trụ tròn
Dưới đây là cách tính thể tích hình trụ tròn:
Thể tích hình trụ tròn được tính bằng diện tích của đáy nhân với chiều cao. Nếu như một hình trụ tròn có bán kính là r cùng với chiều cao là h thì thể tích hình trụ tròn như sau:
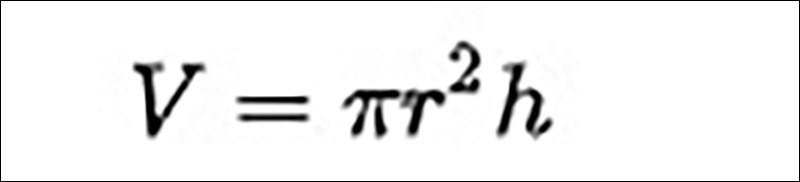
Ví dụ cách tính thể tích hình trụ tròn
Cho một lăng trụ bất kỳ có bán kính mặt đáy r = 4 cm, trong khi đó, chiều cao nối từ đỉnh của hình trụ xuống đáy hình trụ có độ dài h = 8 cm. Hỏi thể tích của hình trụ này bằng bao nhiêu?
Theo đó, ta áp dụng vào công thức tính thể tích hình trụ và có: bán kính mặt đáy hình trụ r = 4cm và chiều cao hình trụ h = 8cm. Suy ra, ta có công thức tính thể tích hình trụ như sau:
V = π x r2 x h = π x 42 x 8 = ~ 402 cm3
Bài tập tính diện tích hình trụ tròn
Ví dụ 1: Có khối trụ với thiết diện qua trục là hình vuông cạnh 2a. Hãy tính diện tích xung quanh, diện tích toàn phần và thể tích của khối trụ này.
Cách giải:
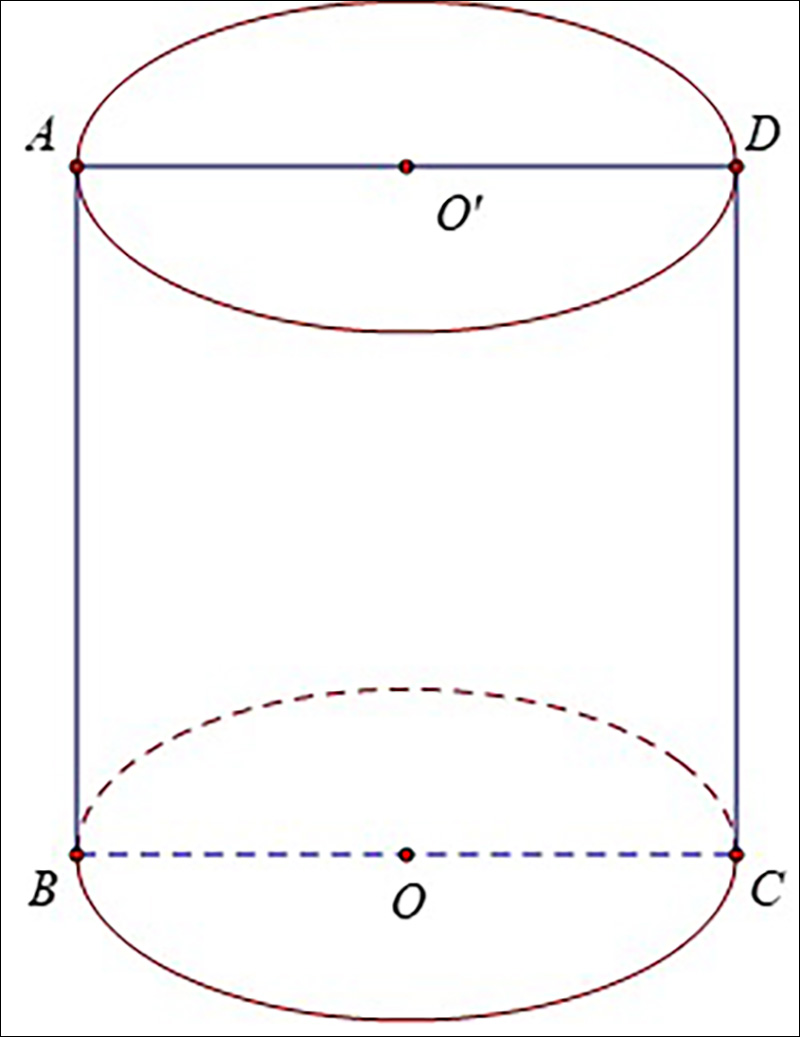
Từ dữ liệu bài toán, ta có thiết diện là hình vuông ABCD cạnh 2a
Đường cao của hình trụ là AB = 2a, và bán kính đáy OB = a.
Diện tích xung quanh của khối trụ là: Sxq= 2πrh=2π.a.2a=4πa2
Diện tích toàn phần của khối trụ là Stp= 2πrh+2πr2=4πa2+2πa2=6πa2
Thể tích của khối trụ đã cho là: V=πr2h=π.a2.2a=2πa3
Ví dụ 2: Một khối trụ có bán kính đáy R = a . Với dữ kiện là thiết diện song song với trục và cách trục khối trụ một khoảng bằng a/2 là hình chữ nhật có diện tích bằng a2 √3 . Hãy tính thể tích khối trụ đó.
Cách giải:
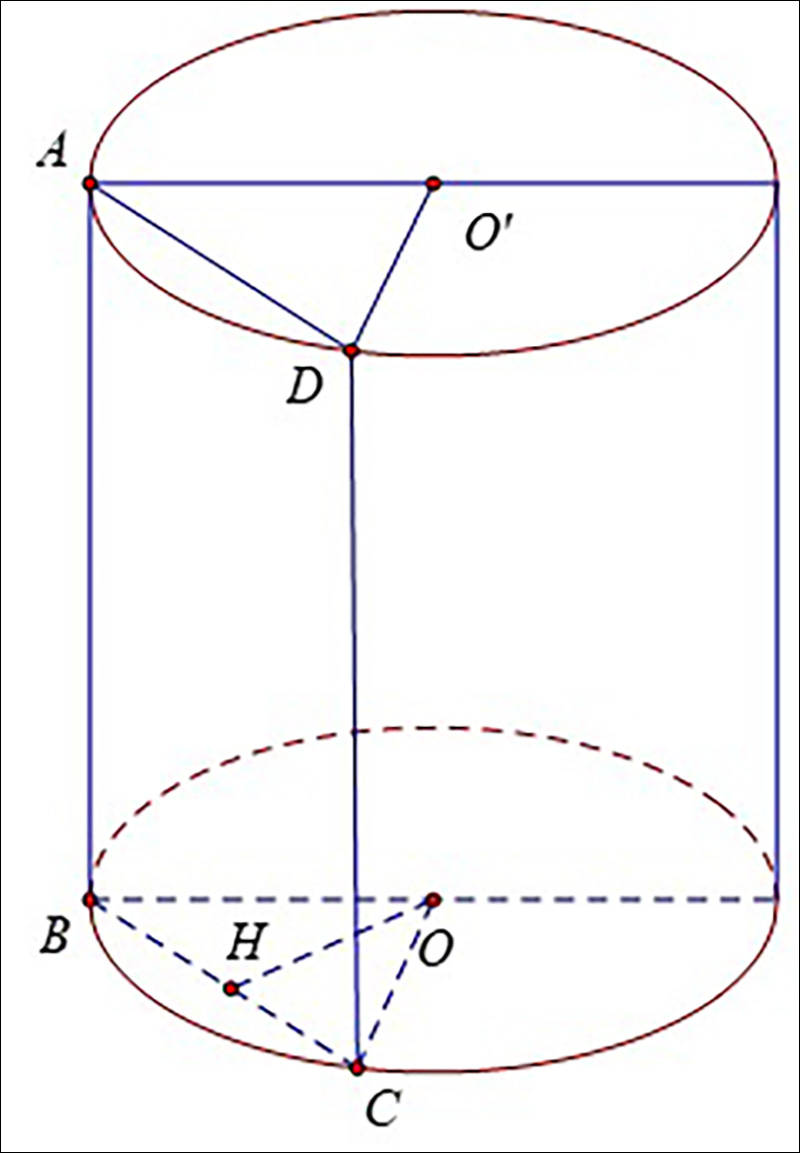
∆BOC cân tại O có OH là đường cao, nên:
⇒ H là trung điểm của BC
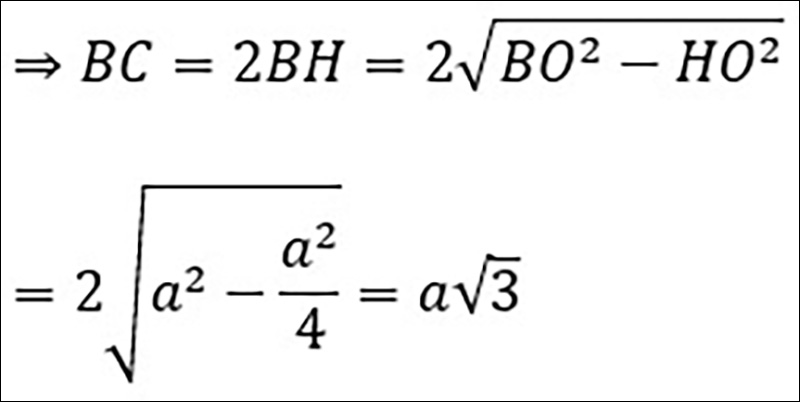
Ta có ABCD là hình chữ nhật nên:
SABCD= AB.BC=AB.a√3=a2√3⇒ AB=a
Thể tích của khối trụ đã cho là:
V=πr2h=π.a2.a= πa3
Ví dụ 3: Tính diện tích toàn phần hình trụ có chiều cao là 8cm và diện tích xung quanh bằng 352 (cm^{2}).
Cách giải:
Ta có h = 8 và (S_{xq} = 352)
(Rightarrow r = frac{S_{xq}}{2pi h} = frac{352}{2.3,14.8} approx 7)
(Rightarrow S_{tp} = 352 + 2.3,14.7^{2} = 659,72)
Xem thêm:
- Diện tích hình tròn và công thức tính diện tích hình tròn
- Thiết diện là gì? Công thức tính thiết diện và Một số bài tập
- Hình nón cụt là gì? Cách tính thể tích hình nón cụt
Trên đây là bài viết về chủ đề diện tích hình trụ tròn và công thức tính diện tích hình trụ tròn trong chương trình toán học lớp 5. Nếu có góp ý, băn khoăn hay thắc mắc gì các bạn để lại bình luận bên dưới nhé! Cảm ơn các bạn. Chúc bạn luôn học tốt nhé!


