Định lý Pytago là một kiến thức quan trọng và cơ bản của hình học, được ứng dụng rộng rãi trong nhiều bài toán, vật lý và cả những điều thực tế ngoài cuộc sống. Vì vậy, bài viết hôm nay chúng ta sẽ cùng tìm hiểu rõ hơn về định lý Pytago nhé.
Nội dung bài viết
Định lý Pytago là gì?
Giới thiệu tổng quan về định lý Pytago
Định lý Pytago được chứng minh lần đầu tiên bởi Pythagoras – một nhà toán học và nhà khoa học Hy Lạp cổ đại. Ông được xem là một trong những người nổi tiếng nhất trong lịch sử loài người, đặt nền móng quan trọng cho nhiều lĩnh vực.
Pythagoras (570-490 TCN) sinh ra trên hòn đảo Samos ở bờ biển phía Tây Hy Lạp, là một người vốn sẵn thông minh và ham học hỏi ông đã trở nên uyên bác rất nhiều lĩnh vực như: số học, hình học, y học, triết học, thiên văn học,…

Xem thêm:
- 1 độ bằng bao nhiêu phút, giây, radian? Cách đổi đơn vị độ (góc)
- Cách đổi inch sang m cực chính xác, nhanh chóng bằng công cụ
- Cách đổi dm sang cm, m, km, inch,… chính xác nhất
- Cách đổi mm sang m chính xác nhất bằng công cụ chuyển đổi
Công thức định lý Pytago
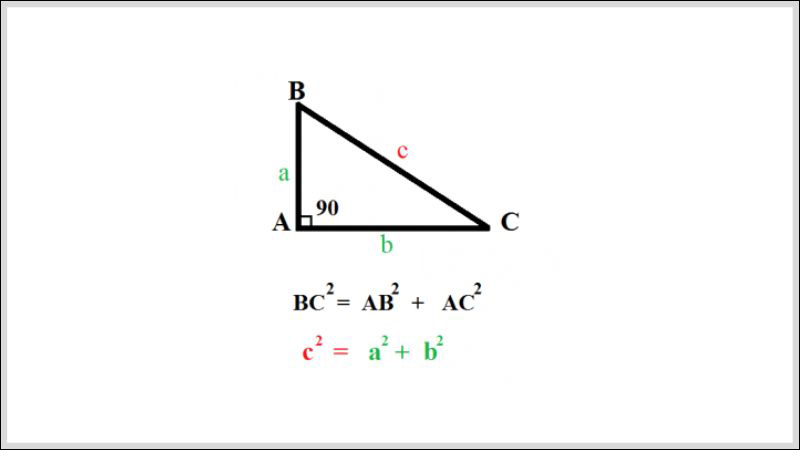
Định lý Pytago được phát biểu chính xác như sau: Trong một tam giác vuông, bình phương cạnh huyền (cạnh đối với góc vuông) bằng tổng bình phương hai cạnh của góc vuông.
Định lý Pytago còn có thể biểu diễn rõ hơn dưới dạng phương trình: Với ABC vuông tại A, gọi độ dài AB, AC, BC lần lượt là a, b, c, ta có phương trình sau:
c² = a² + b²
Định lý Pytago ngược
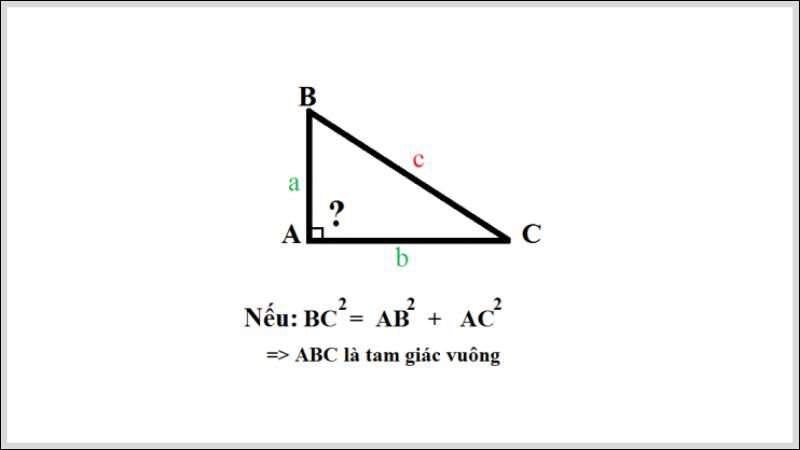
Định lý Pytago ngược được phát biểu: Nếu một tam giác có bình phương của một cạnh bằng tổng bình phương của hai cạnh còn lại thì tam giác đó là tam giác vuông.
Ví dụ: Nếu tam giác ABC có BC² = AB² + AC² thì ABC là tam giác vuông tại A.
Tuy nhiên định lý nghịch đảo có thể được chứng minh bằng cách sử dụng định lý Cos hoặc định lý Pytago dương.
Hệ quả của định lý Pytago
Bộ ba Pytago
Bộ ba Pytago bao gồm ba số nguyên dương a, b, c. Thường được viết là (3, 4, 5), (5, 12, 13) hoặc (a, b, c). Bằng chứng từ các địa điểm khảo cổ ở Bắc u cho thấy những bộ ba này đã được người cổ đại biết đến trước thời điểm được ghi chép lại.
Một bộ ba số nguyên dương được gọi là một bộ ba Pythagore nguyên thủy khi các số a, b và c đồng nguyên tố hoặc ước số chung lớn nhất của a, b và c bằng 1.
Các bộ ba Pythagore nguyên thủy nhỏ hơn 100 là: (3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12 , 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77 , 85), (39, 80, 89), (48, 55, 73), (65, 72, 97).
Số phức
Với mọi số phức (z = x + yi) thì môđun hoặc giá trị tuyệt đối của nó sẽ có dạng:
r = |z| = √(x² + y²)
Vì vậy ta có thể thấy r, x, y liên hệ với nhau theo phương trình Pytago như sau:
r² = x² + y²
Trong đó r được định nghĩa là một số thực dương hoặc số 0 và x, y có thể là số dương hoặc âm.
Trong hình học, r là khoảng cách từ z đến điểm O hoặc gốc tọa độ trong mặt phẳng phức. Nên ta có thể dựa vào định nghĩa để tính khoảng cách giữa hai điểm z1 và z2 như sau:
|z1 – z2| = √(x1-x2)² + (y1 – y2)²
(z1 – z2)² = (x1 – x2)² + (y1 – y2)²
Vậy nên đây cũng là một dạng của Pytago.
Đẳng thức lượng giác Pytago
Với một tam giác vuông có hai cạnh góc vuông a, b và cạnh huyền c thì công thức lượng giác xác định sin và cos của góc giữa cạnh góc vuông a và cạnh huyền như sau:
Sin α = b/c
Cos α = a/c
(Sin α)^2 + (Cos α)^2 = (b/c)^2 + (a/c)^2 = (c/c)^2=1
Mối quan hệ giữa sin và cosin đôi khi được gọi là đồng dạng lượng giác cơ bản của Pytago.
Các ứng dụng của định lý Pytago
Định lý Pytago được áp dụng ở rất nhiều lĩnh vực trong thực tế như:
- Trong xây dựng, thiết kế: Định lý Pytago rất hữu ích khi bạn cần tính toán về độ dài trong các công việc xây dựng hoặc thiết kế. Bạn có thể tính được độ dài cạnh thứ ba khi biết độ dài hai cạnh của một tam giác vuông.
- Trong khoa học, kỹ thuật: Định lý Pytago được sử dụng trong khoa học và kỹ thuật để tính toán khoảng cách giữa hai điểm trên một địa hình hoặc bề mặt. Khi bạn biết chiều cao và độ dài của một cung đường dốc trên một núi, bạn có thể tính toán khoảng cách giữa các điểm trên đường dốc đó bằng định lý Pytago.
- Trong thể thao: Định lý Pytago được sử dụng trong thể thao để tính toán đường chéo của các hình dạng không gian như hộp hoặc lồng. Ví dụ bạn có thể sử dụng định lý Pytago để tính toán đường chéo của sân để biết được khoảng cách từ trung tâm sân bóng đến các góc sân.
- Trong đời sống hàng ngày: Định lý Pytago còn được sử dụng trong đời sống hàng ngày để giải quyết các vấn đề đo lường kích thước trong gia đình hoặc văn phòng. Ví dụ, bạn có thể sử dụng định lý Pytago để tính toán độ dài chéo của của một bức tường hoặc một tấm ván từ đó bạn có thể biết độ dài của nó.

Bài tập ví dụ công thức tính cạnh huyền tam giác vuông
Bài tập 1:
Cho tam giác ABC vuông tại A:
Cho biết độ dài cạnh AB = 5 cm, chiều dài cạnh BC = 6 cm, tính chiều dài cạnh AC
Cho biết chiều dài cạnh AC = 3 cm, chiều dài cạnh BC = 7 cm, tính chiều dài cạnh AB
Cho biết chiều dài cạnh AB = 4 cm, chiều dài cạnh AC = 3 cm, tính chiều dài cạnh BC
Bài giải:
Giải bài tập định lý Pytago thông qua công thức trên.
1. Ta có:
BC² = AC² + AB²
=> AC² = BC² – AB²
=> AC² = 6² – 5²
=> AC = √11
Vậy chiều dài của cạnh AC là √11 cm
2. Ta có:
BC² = AC² + AB²
=> AB² = BC² – AC²
=> AB² = 7² – 3 ²
=> AB = 2√10
Vậy chiều dài cạnh AB = 2√10 cm
3. Ta có:
BC² = AC² + AB²
=> BC² = 3² + 4²
=> BC = 5
Vậy chiều dài cạnh BC là 5
Xem thêm:
- Thiết diện là gì? Công thức tính thiết diện và Một số bài tập
- Hệ tọa độ trong không gian là gì? Công thức và Bài tập ví dụ
- Hình thoi là gì? Cách tính diện tích hình thoi và chu vi hình thoi
Trên đây là toàn bộ lý thuyết về định lí Pytago ý nghĩa và ứng dụng của nó. Hy vọng bài viết cung cấp cho bạn những thông tin hữu ích và đừng quên theo dõi những bài viết khác tại DINHNGHIA nhé!


