Chương trình toán học lớp 11 bao gồm chuyên đề quan trọng về hai mặt phẳng vuông góc. Vậy cụ thể hai mặt phẳng vuông góc là gì? Tính chất 2 mặt phẳng vuông góc? Chuyên đề và bài tập 2 mặt phẳng vuông góc như nào?… Trong bài viết cụ thể dưới đây, hãy cùng DINHNGHIA.VN tìm hiểu nhé!
Chuyên đề hai mặt phẳng vuông góc
Định nghĩa hai mặt phẳng vuông góc là gì?
Nếu 2 mặt phẳng vuông góc với nhau thì góc giữa chúng bằng 90 độ.
(𝑃)⊥(𝑄)⇔((𝑃),(𝑄)ˆ)=90 độ
Điều kiện để 2 mặt phẳng vuông góc
Hai mặt phẳng vuông góc với nhau khi và chỉ khi trong mặt phẳng này và có một đường thẳng vuông góc với mặt phẳng kia.
{𝑑𝑑⊥(𝑄)⊂(𝑃)⇒(𝑃)⊥(𝑄).

Tính chất của hai mặt phẳng vuông góc
- Nếu 2 mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng và vuông góc với giao tuyến cũng vuông góc với mặt phẳng kia.
⎧⎩⎨⎪⎪⎪⎪(𝑃)𝑎(𝑃)𝑎⊥(𝑄)⊂(𝑃)∩(𝑄)=⊥𝑏𝑏⇒𝑎⊥(𝑄)
- Nếu hai mặt phẳng (P), (Q) vuông góc với nhau và thì đường thẳng a qua A và vuông góc với (Q) sẽ nằm trong (P).
⎧⎩⎨⎪⎪⎪⎪(𝑃)𝐴𝐴𝑎⊥(𝑄)∈(𝑃)∈⊥(𝑄)𝑎⇒𝑎⊂(𝑃)
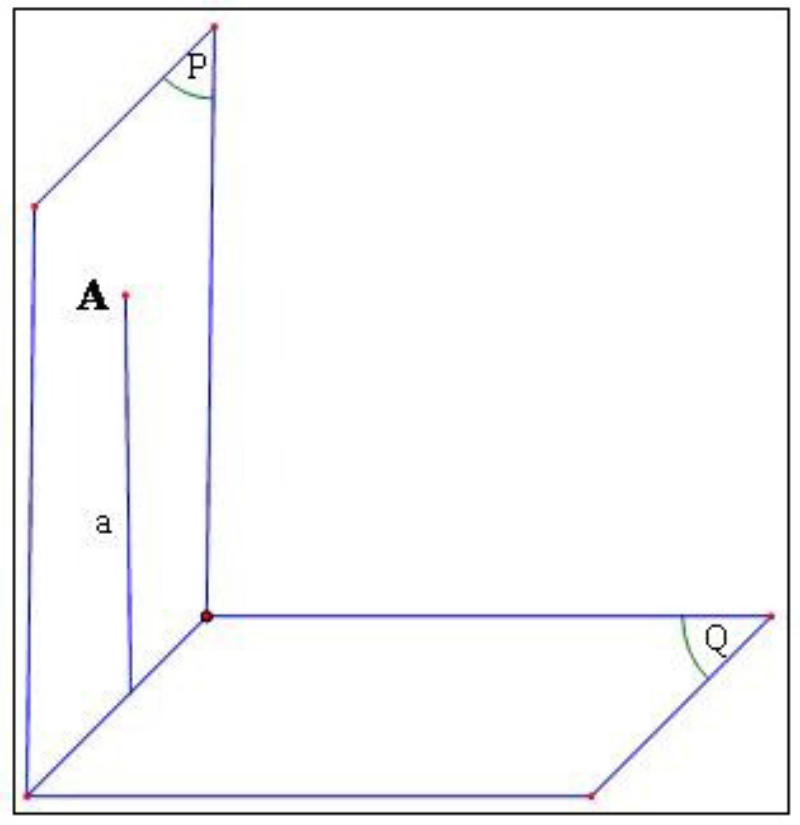
- Nếu hai mặt phẳng cắt nhau và cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng cũng vuông góc với mặt phẳng thứ ba.
⎧⎩⎨⎪⎪(𝑃)(𝑃)(𝑄)∩(𝑄)=𝑎⊥(𝑅)⊥(𝑅)⇒𝑎⊥(𝑅).

Hai mặt phẳng vuông góc trong không gian Oxyz
Phương trình tổng quát mặt phẳng trong không gian Oxyz
Phương trình tổng quát của mặt phẳng (P) trong không gian Oxyz có dạng:
𝐴𝑥+𝐵𝑦+𝐶𝑧+𝐷=0
với 𝐴2+𝐵2+𝐶2>0
Do đó muốn viết phương trình mặt phẳng trong không gian ta phải cần xác định được 2 dữ kiện:
- Điểm M bất kì mà mặt phẳng đã đi qua
- Vector pháp tuyến của mặt phẳng
Điều kiện hai mặt phẳng vuông góc trong không gian Oxyz
Cho 2 mặt phẳng (𝑃):𝐴𝑥+𝐵𝑦+𝐶𝑧+𝐷=0và (𝑄):𝐴′𝑥+𝐵′𝑦+𝐶′𝑧+𝐷′=0
thì ta có 2 mặt phẳng vuông góc khi và chỉ khi: 𝐴𝐴′+𝐵𝐵′+𝐶𝐶′+𝐷𝐷′=0.
Cách chứng minh hai mặt phẳng vuông góc
Chứng minh 2 mặt phẳng vuông góc với nhau
- Cách 1: Chứng minh mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
- Cách 2: Chứng minh góc giữa hai mặt phẳng là 90∘.
Chứng minh đường thẳng d vuông góc với mặt phẳng (𝛼)
- Cách 1: Nếu hai mặt phẳng cùng vuông góc với mặt phẳng thứ ba thì giao tuyến (nếu có) của chúng cũng vuông góc với mặt phẳng này.
- Cách 2: Nếu 2 mặt phẳng vuông góc với nhau, khi một đường thẳng nằm trong mặt phẳng này vuông góc với giao tuyến thì vuông góc với mặt phẳng kia.
Kết quả:
- 𝑆′=𝑆𝑐𝑜𝑠𝜑
- Nếu hai mặt phẳng (P) và (Q) vuông góc với nhau, điểm A thuộc mặt phẳng (P) thì mọi đường thẳng qua A và vuông góc với (Q) đều nằm trong (P).
Các dạng bài tập hai mặt phẳng vuông góc
Bài tập hai mặt phẳng vuông góc cơ bản
Cho hình chóp𝑆𝐴𝐵𝐶 có đáy ABC là tam giác vuông tại B, Gọi H, K lần lượt là hình chiếu vuông góc của A trên SB, SC. Chứng minh rằng: (𝑆𝐴𝐵)⊥(𝑆𝐵𝐶),(𝐴𝐻𝐾)⊥(𝑆𝐵𝐶).
Cách giải:
- Chứng minh (𝑆𝐴𝐵)⊥(𝑆𝐵𝐶):
Để chứng minh 2 mặt phẳng vuông góc với nhau, ta chứng minh trong mặt phẳng này có 1 đường thẳng vuông góc với mặt phẳng kia.
Ta có: Tam giác ABC vuông tại B ⇒𝐴𝐵⊥𝐵𝐶(1).
𝑆𝐴⊥(𝐴𝐵𝐶)⇒𝑆𝐴⊥𝐵𝐶(2).
Từ (1) và (2) ⇒𝐵𝐶⊥(𝑆𝐴𝐵),𝐵𝐶⊂(𝑆𝐵𝐶)⇒ (𝑆𝐴𝐵)⊥(𝑆𝐵𝐶)
(đpcm).
- Chứng minh(𝐴𝐻𝐾)⊥(𝑆𝐵𝐶):
Ta có: 𝐵𝐶⊥(𝑆𝐴𝐵)⇒𝐵𝐶⊥𝐴𝐻(3).
H là hình chiếu vuông góc của A (gt) ⇒𝑆𝐵⊥𝐴𝐻(4).
Từ (3) và (4) ⇒𝐴𝐻⊥(𝑆𝐵𝐶),𝐴𝐻⊂(𝐴𝐻𝐾)⇒(𝐴𝐻𝐾)⊥(𝑆𝐵𝐶) (đpcm).

Bài tập hai mặt phẳng vuông góc trong không gian
Bài 4 SGK toán 11 2 mặt phẳng vuông góc
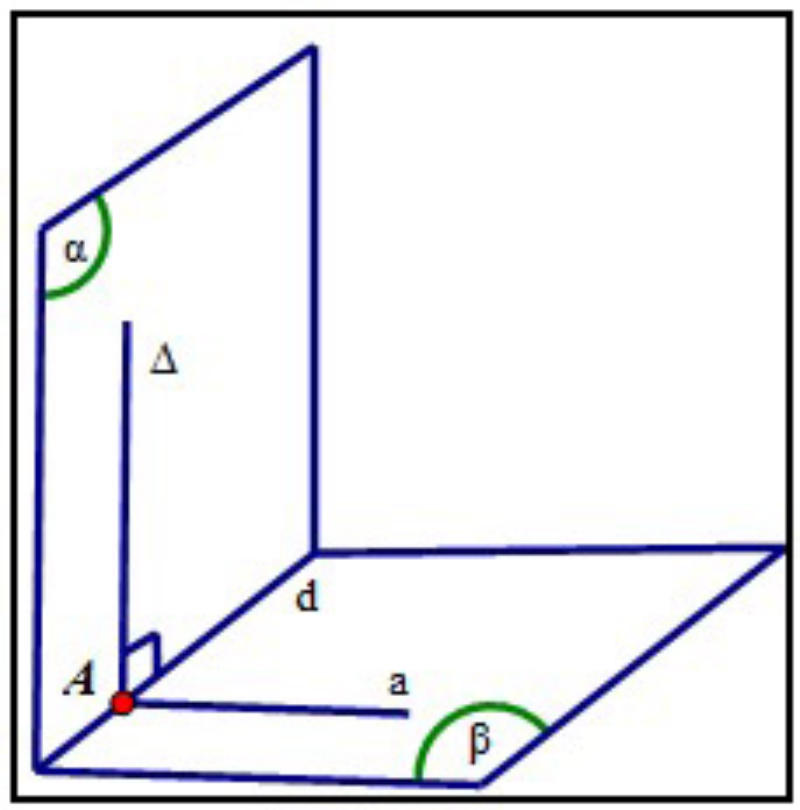
Cho hai mặt phẳngΔ và (𝛽) vuông góc với nhau và cắt nhau theo giao tuyến d. Chứng minh rằng nếu có một đường thẳng Δ nằm trong Δ và Δ vuông góc với d thì Δ vuông góc với (𝛽).
Cách giải:
Ta có:
{ΔΔ⊂⊥(𝛼)𝑑⇒Δ∩𝑑={𝐴}
Từ A, kẻ đường thẳng a: {𝑎𝑎∈⊥(𝛽)𝑑
Do (𝛼)⊥(𝛽)⇒((𝛼),𝑎ˆ)=90∘ hay Δ⊥𝑑
Từ đó suy ra: Δ⊥(𝑑,𝑎) hay Δ⊥(𝛽)
Xem thêm:
- Định nghĩa hai đường thẳng vuông góc lớp 7: Lý thuyết và Bài tập
- Thiết diện là gì? Công thức tính thiết diện và Một số bài tập
- Khoảng cách giữa 2 đường thẳng là gì? Cách tính khoảng cách giữa 2 đường thẳng
Như vậy, bài viết trên đây của DINHNGHIA.VN đã giúp bạn tổng hợp kiến thức về chủ đề hai mặt phẳng vuông góc. Chúc bạn luôn học tốt!Hai mặt phẳng vuông góc là gì? Bài tập 2 mặt phẳng vuông góc
