Nhận dạng đồ thị hàm số là dạng toán mới nhưng rất hay gặp trong các bài toán thi THPT Quốc gia. Vậy cần lưu ý gì về cách nhận dạng đồ thị hàm số? Có những loại hàm số nào? Cách nhận dạng đồ thị hàm số mũ và logarit? Bài tập trắc nghiệm nhận dạng đồ thị hàm số? Phân biệt các dạng đồ thị hàm số?… Trong nội dung bài viết dưới đây, DINHNGHIA.VN sẽ giúp bạn tổng hợp kiến thức về chủ đề “cách nhận dạng đồ thị hàm số”, cùng tìm hiểu nhé!
Cách nhận dạng đồ thị hàm số đa thức
Hàm số đa thức là hàm số có dạng anxn+an−1xn−1+…+a1x+a0 với an;an−1;…a1;a0∈R
Một số tính chất của hàm số đa thức như sau:
- Hàm số đa thức bậc n sẽ có tối đa n nghiệm phân biệt
- Hàm số luôn đi qua điểm M(0;a0)
- Nếu an>0 thì limx→+∞=+∞
- Nếu an<0 thì limx→+∞=–∞
Như vậy tùy vào bậc của hàm số mà ta có các tính chất riêng trong cách nhận dạng đồ thị của hàm số.
Cách nhận biết đồ thị hàm số bậc nhất
Hàm số bậc nhất là hàm số có dạng y=ax+b với a≠0
- Đồ thị hàm số là một đường thẳng cắt trục tung tại điểm có tung độ bằng b và cắt trục hoành tại điểm có hoành độ là −ba
- Từ kiến thức về cách nhận dạng đồ thị hàm số thì để nhận biết hàm số đã cho, ta chia mặt phẳng Oxy ra làm bốn góc phần tư.

- Nếu đồ thị là đường thẳng cắt ngang qua hai đoạn của góc phần tư 1 hoặc 3 thì hàm số có a<0
- Nếu đồ thị là đường thẳng cắt ngang qua hai đoạn của góc phần tư 2 hoặc 4 thì hàm số có a>0
Ví dụ:
Cho đồ thị như hình vẽ. Hãy cho biết đây là đồ thị của hàm số nào.

Cách giải:
Vì đồ thị là một đường thẳng nên ⇒ đây là đồ thị hàm số bậc nhất.
Giả sử hàm số là y=ax+b
Do hàm số cắt trục tung tại điểm có tung độ bằng 1⇒b=1
Hàm số cắt trục hoành tại điểm có hoành độ bằng 3⇒−ba=3⇒a=−1/3
Vậy hàm số là y=−x/3+1
Cách nhận biết đồ thị hàm số bậc 2
Hàm số bậc hai là hàm số có dạng y=ax^2+bx+c với a≠0
Đồ thị hàm số bậc hai là một Parabol cắt trục tung tại điểm có tung độ bằng c (đỉnh của Parabol), nhận đường thằng x=−b/2a làm trục đối xứng. Cách nhận dạng đồ thị hàm số bậc 2 cụ thể như sau:
- Parabol có đỉnh ở phía trên khi a<0
- Và Parabol có đỉnh ở phía dưới khi a>0
Ví dụ:
Cho hàm số bậc hai có đồ thị như hình vẽ. Hãy xác định hàm số đó.

Cách giải:
Giả sử hàm số là y=ax^2+bx+c
Hàm số cắt trục tung tại điểm có tung độ bằng 1⇒c=1
Hàm số nhận đường thẳng x=−2 làm trục đối xứng ⇒−b/2a=−2⇔b=4a
Do hàm số đi qua điểm (−1;−2) nên ta có:
−2=a−b+1⇒−2=a−4a+1
⇒3a=3⇒a=1;b=4
Vậy hàm số là y=x^2+4x+1
Cách nhận biết đồ thị hàm số bậc 3
Hàm số bậc 3 là hàm số có dạng:
y=ax^3+bx^2+cx+d với a≠0
- Hàm số cắt trục tung tại điểm có tung độ bằng d
- Hàm số cắt trục hoành tại 1 điểm hoặc 3 điểm
Cách nhận dạng đồ thị hàm số bậc 3 thì chúng ta nhận biết dạng của đồ thị qua số tiệm cận của hàm số bằng cách xét đạo hàm y′=3ax^2+2bx+c
Trường hợp 1: Phương trình y′=0 có hai nghiệm phân biệt
Khi đó đồ thị hàm số có hai điểm cực trị và có hình dạng như sau.
Trường hợp 2: Phương trình y′=0 có một nghiệm kép
Khi đó đồ thị hàm số không có điểm cực trị và tiếp tuyến tại điểm uốn song song với trục hoành.
Trường hợp 3: Phương trình y′=0 vô nghiệm
Khi đó đồ thị hàm số không có điểm cực trị nhưng tiếp tuyến tại điểm uốn không song song với trục hoành.
Ví dụ:
Cho hàm số bậc ba y=ax^3+bx^2+cx+d có đồ thị như hình vẽ.
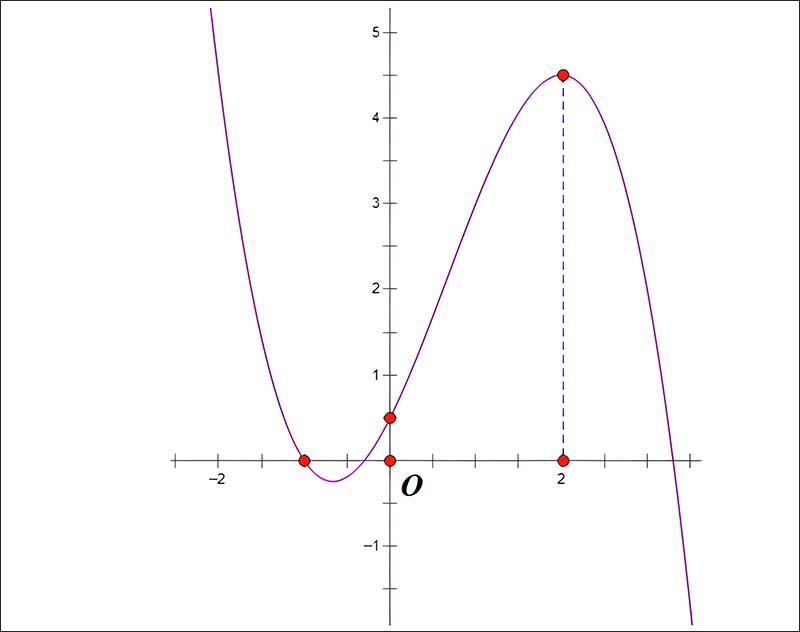
Hãy xét dấu của a;b;c;d
Cách giải:
Do đồ thị cắt trục tung tại điểm có tung độ >0 nên ⇒d>0
Do limx→+∞y=−∞⇒a<0
Nhìn vào đồ thị dễ thấy : Hàm số có hai điểm cực trị x1;x2 thỏa mãn
- −1<x1<0
- x2=2
Suy ra:
- x1+x2>0
- x1x2<0
Xét đạo hàm y′=3ax^2+2bx+c
Do x1;x2 là hai nghiệm của phương trình y′=0 nên theo định lý Viet ta có :
- x1+x2=−2b
- 6a>0
- x1x2=c
- 3a<0
Do a<0 nên:
⇒b>0
c>0
Vậy a<0 và b;c;d>0
Cách nhận diện đồ thị hàm số bậc 4 trùng phương
Hàm số bậc 4 trùng phương là hàm số có dạng :
y=ax^4+bx^2+c với a≠0
- Hàm số cắt trục tung tại điểm có tung độ bằng c
- Hàm số luôn nhận trục tung làm trục đối xứng
Cách nhận dạng đồ thị hàm số bậc 4 trùng phương thì chúng ta nhận biết dạng của đồ thị qua số tiệm cận của hàm số bằng cách xét đạo hàm y′=4ax^3+2bx
Trường hợp 1: Phương trình y′=0 có 3 nghiệm phân biệt.
Khi đó đồ thị hàm số có 3 điểm cực trị.
Trường hợp 2 : Phương trình y′=0 có duy nhất 1 nghiệm
Khi đó đồ thị hàm số có 1 điểm cực trị và có hình dáng giống với đồ thị Parabol.
Để phân biệt trường hợp này với đồ thị Parabol ta cần lưu ý chú ý sau :
Hàm số trùng phương luôn nhận trục tung làm trục đối xứng. Do đó nếu đồ thị có dạng Parabol có trục đối xứng khác trục tung thì đó là hàm số bậc 2
Ví dụ:
Cho đồ thị hàm số bậc 4 như hình vẽ. Xác định hàm số.

Cách giải:
Dễ thấy hàm số đối xứng qua trục tung nên đây là hàm số bậc 4 trùng phương y=ax^4+bx^2+c
Do hàm số cắt trục tung tại gốc tọa độ nên ⇒c=0
Do hàm số đi qua hai điểm (1;−1);(2–√;0) nên thay vào ta được :
- a+b=−1
- 4a+2b=0
Suy ra:
- a=1
- b=−2
Vậy hàm số là y=x^4−2x^2
Nhận dạng một số đồ thị hàm số đặc biệt
Cách nhận dạng đồ thị hàm số phân thức
Hàm số phân thức là hàm số có dạng y=ax+b/cx+d
Cách nhận dạng đồ thị hàm số phân thức: Đồ thị hàm số phân thức gồm hai đường cong nằm ở hai góc phần tư đối xứng nhau trên trục tọa độ
Đồ thị hàm số cắt trục tung tại điểm (0;b/d), cắt trục hoành tại điểm (−b/a;0)
Hàm số có hai đường tiệm cận:
- Tiệm cận ngang y=ac
- Tiệm cận đứng x=−dc
Tùy thuộc vào giá trị đạo hàm y′=ad−bc(cx+d)2 mà đồ thị có hai dạng khác nhau.
Vậy ta có một số chú ý sau để xét nhanh các giá trị của tham số:
- Hàm số giao với trục Ox tại điểm nằm phía bên phải gốc tọa độ ⇒ab<0
- Hàm số giao với trục Ox tại điểm nằm phía bên trái gốc tọa độ ⇒ab>0
- Hàm số không cắt trục Ox⇒a=0
- Tiệm cận ngang nằm phía trên trục Ox⇒ac>0
- Tiệm cận ngang nằm phía dưới trục Ox⇒ac<0
- Tiệm cận ngang trùng trục Ox⇒a=0
- Hàm số giao với trục Oy tại điểm nằm phía bên trên gốc tọa độ ⇒bd>0
- Hàm số giao với trục Oy tại điểm nằm phía bên dưới gốc tọa độ ⇒bd<0
- Hàm số giao Oy tại điểm trùng gốc tọa độ ⇒b=0
- Tiệm cận đứng nằm bên phải trục Oy⇒cd<0
- Tiệm cận đứng nằm bên trái trục Oy⇒cd>0
- Tiệm cận đứng trùng với trục Oy⇒d=0
Ví dụ:
Cho hàm số y=ax+bcx+d có đồ thị như hình vẽ

Nhận xét dấu của ad và bc
Cách giải:
Dễ thấy đồ thị là nghịch biến và có hai đường tiệm cận dương nên ta có :
ad−bc<0;ac>0;−dc>0⇔ac>0;dc<0;ad−bc<0
Do ac>0;dc<0 nên ⇒ad<0
Hàm số cắt trục tung tại điểm có tung độ <0⇒bd<0⇒bd<0
Mà cd<0⇒bd.cd=bc;d2>0⇒bc>0
Vậy ad<0;bc>0
Cách nhận dạng đồ thị hàm số mũ và logarit
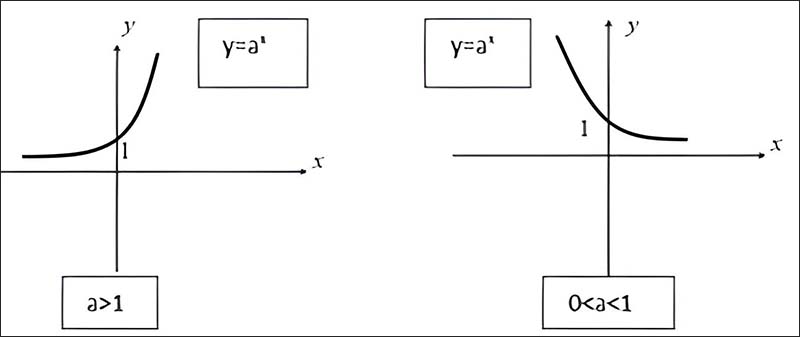
Hàm số mũ là hàm số có dạng y=ax với a>0;a≠1
Cách nhận dạng đồ thị hàm số mũ: Đồ thị hàm số mũ là một đường cong luôn nằm phía trên trục hoành.
Đồ thị hàm số mũ cắt trục tung tại điểm (0;1), luôn đi qua điểm (1;a) , luôn nằm phía trên trục hoành và nhận trục hoành làm tiệm cận ngang.
Tùy theo giá trị của a mà có hai dạng đồ thị khác nhau:
Hàm số Logarit là hàm số có dạng y=logax với a>0;a≠1
Cách nhận dạng đồ thị hàm số logarit: Đồ thị hàm số Logarit là một đường cong nằm phía bên phải trục tung.
Đồ thị hàm số logarit cắt trục hoành tại điểm (1;0) , luôn đi qua điểm (a;1) , luôn nằm phía bên phải trục tung và nhận trục tung làm tiệm cận đứng
Tùy theo giá trị của a mà có hai dạng đồ thị khác nhau:
Ví dụ 1:
Tìm giá trị của a để hàm số y=logax có đồ thị là hình dưới đây.
Cách giải:
Vì hàm số đi qua điểm (2;2) nên ta có :
loga2=2⇒a2=2⇒a=2
Vậy hàm số là y=log2√2
Ví dụ 2:
Đồ thị dưới đây là của hàm số nào?
Cách giải:
Ta thấy đồ thị là một đường cong nằm phía trên trục hoành ⇒ đây là đồ thị hàm số mũ y=ax
Vì đồ thị đi qua điểm (−1;3) nên ta có :
a−1=3⇔1a=3⇔a=13
Vậy hàm số là y=(13)x
Cách nhận biết đồ thị hàm số lượng giác
Hàm số lượng giác là những hàm số đặc trưng bởi tính tuần hoàn. Có bốn hàm số lượng giác cơ bản, từ các tính chất của từng hàm số lượng giác thì ta sẽ có cách nhận dạng đồ thị hàm số lượng giác riêng.
Hàm số y=sinx
- Hàm số có miền giá trị từ −1 đến 1
- Hàm số tuần hoàn với chu kì 2π
- Hàm số là hàm số lẻ: sin(−x)=–sinx
- Cách nhận dạng đồ thị hàm số y=sinx: Đồ thị hàm số có dạng sóng đi qua gốc tọa độ, nằm giữa hai đường thẳng y=−1 và y=1
Hàm số y=cosx
- Hàm số có miền giá trị từ −1 đến 1
- Hàm số tuần hoàn với chu kì 2π
- Hàm số là hàm số chẵn: cos(−x)=cosx
- Cách nhận dạng đồ thị hàm số y=cosx: Đồ thị hàm số có dạng sóng không đi qua gốc tọa độ và đi qua điểm (0;1) , nằm giữa hai đường thẳng y=−1 và y=1
Hàm số y=tanx
- Hàm số được xác định bởi công thức y=sinxcosx
- Hàm số tuần hoàn với chu kì π
- Hàm số là hàm số lẻ : tan(−x)=−tanx
- Cách nhận dạng đồ thị hàm số y=tanx: Đồ thị hàm số có dạng những đường sóng không cắt nhau, đối xứng với nhau qua trục hoành.
- Mỗi đường sóng lần lượt đi qua và nhận các điểm có tọa độ (kπ;0) làm tâm đối xứng. Hàm số có xu hướng tiến xuống dưới khi x tăng dần
- Hàm số nhận các đường thẳng x= (k +1/2*pi) làm tiệm cận đứng.

Hàm số y=cotx
- Hàm số được xác định bởi công thức y=cosxsinx
- Hàm số tuần hoàn với chu kì π
- Hàm số là hàm số lẻ: cot(−x)=−cotx
- Cách nhận dạng đồ thị hàm số y=cotx: Đồ thị hàm số có dạng những đường sóng không cắt nhau, đối xứng với nhau qua trục hoành.
- Mỗi đường sóng lần lượt đi qua và nhận các điểm có tọa độ \( ((k +\frac{1}{2})\pi ;0) \) làm tâm đối xứng. Hàm số có xu hướng tiến xuống dưới khi x tăng dần
- Hàm số nhận các đường thẳng x=kπ làm tiệm cận đứng.
Ví dụ:
Hãy cho biết hình vẽ dưới đây là đồ thị của hàm số nào?
Cách giải:
Từ đồ thị ta có một vài nhận xét:
Hàm số có tính tuần hoàn
Hàm số luôn nằm giữa hai đường thẳng y=0 và y=1
Hàm số đi qua gốc tọa độ
Từ những nhận xét trên ta thấy đây là đặc điểm của hàm số y=sinx
Tuy nhiên do hàm số luôn nằm phía trên trục hoành
⇒ Hàm số đó là y=|sinx|
Bài tập trắc nghiệm nhận dạng đồ thị hàm số
Sau đây là một số bài tập trắc nghiệm nhận dạng đồ thị hàm số để các bạn tự luyện tập.
Bài 1:
Hàm số y=ax4+bx2+c có đồ thị như hình vẽ dưới đây. Hãy chọn nhận xét đúng:
A. a<0;b>0;c<0
B. a<0;b<0;c<0
C. a>0;b<0;c<0
D. a<0;b>0;c>0
Đáp số : D
Bài 2:
Tìm giá trị của a;c;d để hàm số y=ax+2cx+d có đồ thị như hình vẽ dưới đây.
A. a=2;c=−1;d=2
B. a=1;c=−1;d=1
C. a=1;c=1;d=2
D. a=1;c=−1;d=2
Đáp số : D
Bài 3:
Hình vẽ dưới đây là đồ thị của hàm số nào?

A. y=log2x
B. y=|log2x|
C. y=log2√x
D. y=|log2√x|
Đáp số : D
Bài 4:
Cho các số thực dương a;b≠1. Biết rằng bất kì đường thẳng nào song song với Ox mà cắt đồ thị hai hàm số y=ax; y=b2 và trục tung lần lượt tại M;N;A thì ta luôn có : AN=2AM . Hãy tìm mối quan hệ a;b
A. b=2a
B. a2=b
C. ab=12
D. ab2=1
Đáp số : D
Bài 5 :
Cho ba đồ thị hàm số y=ax;y=bx;y=cx như hình vẽ với 0<a;b;c≠1. Hãy so sánh ba số a;b;c
A. a<c<b
B. c<a<b
C. b<c<a
D. a<b<c
Đáp số : D
Xem thêm:
- Hàm số mũ là gì? Định nghĩa và Tính chất của hàm số mũ
- Tâm đối xứng của đồ thị hàm số: Lý thuyết và Các dạng bài tập
- Chuyên đề tính giá trị của biểu thức: Lý thuyết và Bài tập vận dụng
Bài viết trên đây của DINHNGHIA.VN đã giúp bạn tổng hợp lý thuyết cũng như bài tập về chuyên đề cách nhận dạng đồ thị hàm số. Bên cạnh đó, các dạng toán nhận dạng đồ thị hàm số cũng được chúng tôi giới thiệu đầy đủ và chi tiết trong nội dung trên. Hy vọng những kiến thức trong bài viết sẽ giúp ích cho bạn trong quá trình học tập và nghiên cứu về chủ đề cách nhận dạng đồ thị hàm số. Chúc bạn luôn học tốt!
